Chapter 14: Indexing

Basic Concepts

Def. Search key is an attribute or a set of attributes used to look up records.

Why we need indexing mechanisms. We create a DB indexed file instructor and its index file. The file instructor is logically a sequential file, but its records may be stored non-contiguously or non-ordered on disk.

Def. An index file consists of records (called index entries) of the form below.

search key	pointer
…	…

Table 1: index file form

Def. Indexing is the process of mapping from search key to storage locations of the records in disk (search key \(\to\) storage locations).

DBS files with indexing mechanism include:

• Indexed file, in which data records are stored.
• Index file, in which index entries are included.

Review: The indexed file can be organized (sequential file, heap file, hash file, clustering file).

Def. Ordered indices, a kind of indexing. In ordered indices, search key and address of the records are stored in sorted order.

search key	pointer
\(S_1\)	…
\(S_2\)	…
\(S_3\)	…
\(S_4\)	…

Table 2: example index file with ordered indices

Def. Hash Indices. Hash function maps search key to the address of the records.

• The records are stored in buckets.
• The number of buckets is the address of the records.
• Determined by hash function.

Ordered indexing Vs Hashing

Expected queries:

• Hashing is better at retrieving records having a specified value of the key.
• If range queries are common, the ordered indices are to be preferred. (Hashing index does not support range query)

*The Primary/Clustering Index

Def. The Primary/Clustering Index (in the index file)

• The search key of the index specifies the sequential order of the indexed file.
• The indexed file is a sequential file.

聚集索引：索引文件搜索键所规定顺序与被索引文件纪录顺序一致。

主索引：

• 建立在主键的索引：当表定义了主键后，DBMS 自动为该表在主键上建立聚集索引，该索引又是主索引。
• 主索引一定是聚集索引，但聚集索引不一定是主索引。
• \(1\) 个表上只能建立 \(1\) 个聚集索引，也只能有 \(1\) 个主索引。
• 如果表没有定义主键，不会有主索引；但可以为该表建立聚集索引。

在没有定义主键的关系表中插入数据：在关系表所在数据库文件中，各个记录顺序一般是无序的，取决于数据插入顺序（heap 文件）。但在有主键的关系表中插入数据：数据库文件是有序的，按照主键顺序排列。

Example: the data file instructor is stored in order of ID (the primary key).

• sequential scanning of ID of the first six tuples/records, i.e. 10101-33456, will fetch block \(n\) and block \(n + 1\)
• sequential scanning on salary of the first six tuples/records, i.e. 40000-75000, will fetch block \(n\), \(n + 1\), \(n + 2\), \(n + 3\)

*The Secondary/Non-Clustering Index

Def. The Secondary/Non-Clustering Index

• A search key specifies an order different from the sequential order of the file.
• Secondary indices have to be dense indices

Index record points to a bucket that contains pointers to the actual records with that particular search key value.

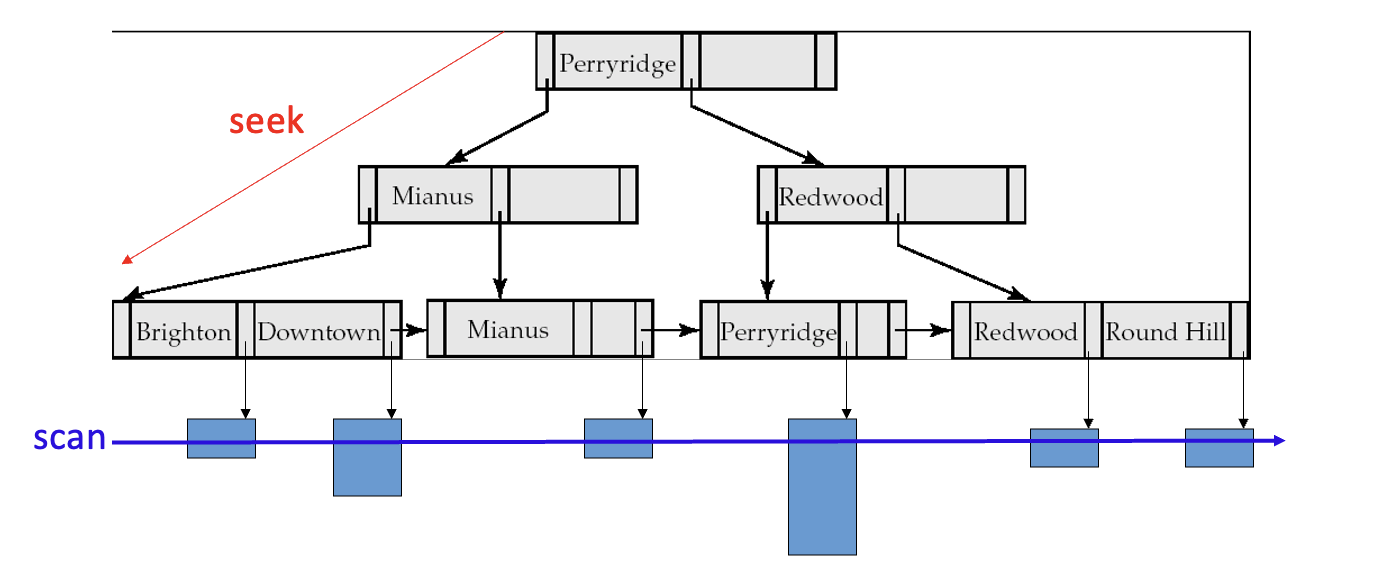
Def. Index-Sequential File. Ordered sequential file with a primary/clustering index on the search key.

1. Sequential scan using primary index is efficient.
2. Sequential scan using secondary index is expensive. This is because each record access may fetch a new block from disk.

Example.

• A DB file is made up of the \(128\)-byte fix-sized logical records. It is stored on disk in unit of block that is of \(1024\)-byte in size.
• The size of the file is \(10240\)-byte.
• Physical I/O operations transfer data on disk into an DBMS buffer in main memory, in terms of \(1024\)-byte block.

If a transaction issues read requests in a sequential access manner, what is the percentage of read requests that result in I/O operations?

• The file contains \(10240 / 128 = 80\) records.
• A block holds \(1024 / 128 = 8\) records.
• The file is stored in \(10240 / 1024 = 10\) blocks.
• Percentage \(= 1 / 8 = 12.5 \%\)

按照记录存储顺序，依次访问每个记录时，每个记录的访问都对应一个 I/O 请求。每次 I/O 访问，DBMS 将 1 个 block 中的 8 个记录读取到内存 buffer 中，即当后续再访问这 8 个记录时，直接从 buffer 中读，无需访问 disk，即无需 I/O 访问。每 8 个 I/O 请求导致 1 个实际 I/O 操作。

Dense and Sparse Indices

Def. Dense Index

• The index record appears for every search key value in the indexed file.
• Each value of search key corresponds to an index entry in the index file.

For dense primary index, the index record contains the search key value.

• A pointer to the first record according to that search key value.
• The rest of the records with the same search key value would be stored sequentially after the first record.

Def. Sparse Index Index file contains index entries for only some search key values.

For sparse index, to locate a file record with the search key value \(K\).

• Find index entry with the largest search key value \(\leq K\).
• Search file sequentially starting at the record to which this index entry points.

Multi-level Indices

The index file may be very large, and cannot be entirely kept in memory. If primary index does not fit in memory, access becomes expensive.

Solution: Treat primary index kept on disk as a sequential file and construct a sparse index on it.

• Outer index - a sparse index of primary index file.
• Inner index - the primary index file.

If even outer index is too large to fit in main memory, yet another level of index can be created, and so on.

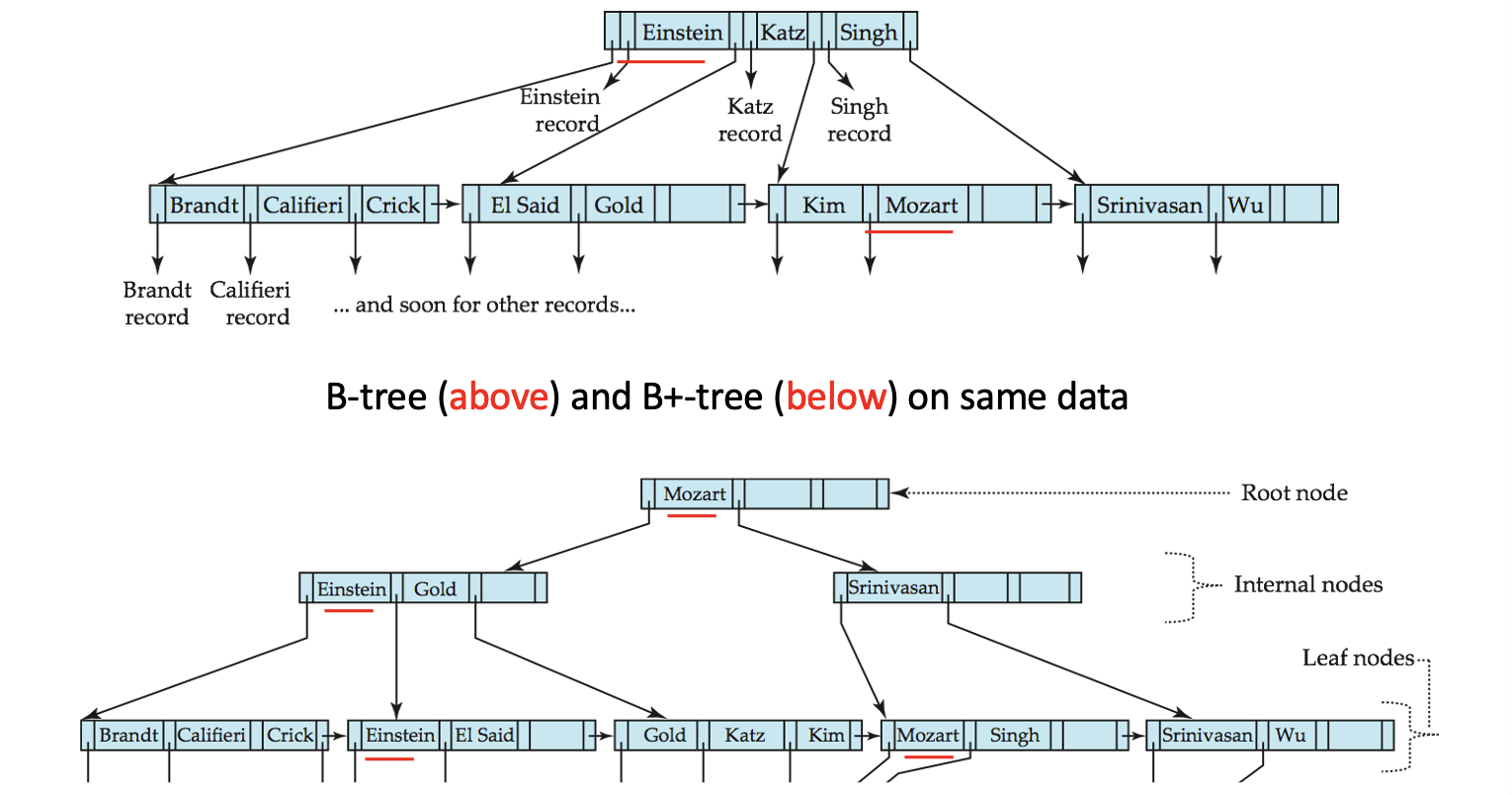
B⁺-tree Properties

Def. B⁺-tree is a rooted tree, with the parameter degree (branching) factor \(n\). All paths from root to leaf are of the same length: balanced tree.

• Each internal node (not root or leaf) has bewteen \(\lceil n / 2\rceil\) and \(n\) children.
• Each leaf node has bewteen \(\lceil (n - 1) / 2\rceil\) and \(n - 1\) search key values.
• Special cases for the root:
  • If the root is not a leaf, it has at least 2 children.
  • If the root is a leaf, it has between 0 and \(n - 1\) values.

Advantages:

• Since the inter-node connections are done by pointers, logically close blocks need not be physically close.
• The non-leaf levels of B⁺-tree form a hierarchy of sparse indices. If there are \(K\) search key values, the height is no more than \(\lceil \log_{\lceil n/2 \rceil}(K)\rceil\)

B⁺-tree Node Structure

The search keys in a node are ordered.

\(P_1\)	\(K_1\)	\(P_2\)	\(K_2\)	\(\cdots\)	\(P_{n - 1}\)	\(K_{n - 1}\)	\(P_{n}\)

Table 3: typical B⁺-tree node structure

• \(K_i\) are the search key values.
• \(P_i\) are
  • pointers to childer (non-leaf nodes).
  • pointers to records or buckets of records (leaf nodes).

Leaf Nodes in B⁺-tree

Leaf node properties

• \(P_i\) points to a record with search key value \(K_i\), \(i < n - 1\).
• \(P_n\) points to the next leaf node.

If \(L_i\), \(L_j\) are leaf nodes, such that \(i < j\), \(L_i\)’s search key values are less than or equal to \(L_j\)’s search key values.

Non-leaf Nodes in B⁺-tree

Non-leaf nodes with \(n\) pointers form a multi-level sparse index on leaf nodes.

1. \(P_1\): The search keys to which \(P_1\) points have values. \(P_1 < K_1\).
2. \(P_i\): The search keys to which \(P_i(2 \leq i \leq n - 1)\), points have values. \(K_{i - 1} \leq P_{i} < K_i\).
3. \(P_n\): The search keys to which \(P_n\) points have values. \(K_{n - 1} \leq P_{n}\).

Non-unique Keys

Def. Non-Unique Keys. If a search key \(a_i\) is not unique, create an index on a composite key\((a_i, A_p)\), which is unique. \(A_p\) could be a primary key, or any other attribute that guarantees uniqueness.

Search for \(a_i = v\) by a range search on composite key. More I/O operations are needed to fetch the actual records

• if the index is clustering, all accesses are sequential
• if the index is non-clustering, each record access may need an I/O operation

Note：MySQL 数据库中，索引树 \(n \leq 100\)，一张表可支持 \(10\) 已行数据，但为了控制 B⁺-tree 索引深度，一般不超过 \(2000\) 万行。其中的原因是

• B⁺-tree 索引（非叶子结点）需要全部调入内存
• B⁺-tree 深度与索引树中非叶子结点数目 \(S\) 所占内存空间取决于表中不同 search-key 数目，如 instructor 表中 ID 的数目
• 假设系统分配给数据库系统可用内存大小为 \(M\)，要求 \(S \leq M\)
• 根据内存 \(M\)、索引树节点大小 \(n\) 值可以确定关系表中的行数

B-tree Index Files

Def. B-tree allows search key values to appear only once.

Non-Leaf nodes: search keys appear nowhere else.

• An additional pointer field for each search key must be included.
• Pointer \(B_i\) are the bucket or the record pointer to leaf node.

\(P_1\)	\(B_1\)	\(K_1\)	\(P_2\)	\(B_2\)	\(K_2\)	\(\cdots\)	\(P_{n - 1}\)	\(B_{n - 1}\)	\(K_{n - 1}\)	\(P_{n}\)

Table 4: typical B-tree node structure

• Advantages: less tree nodes and find search key value before reaching leaf node.
• Disadvantages:
  • Only small fraction of all serach key are found early.
  • Fan-out is reduced, as non-leaf nodes are larger.
  • Insertion and deletion are more complicated.

Comparison between B tree and B+ tree

Figure 1: B-tree above and B⁺-tree below on same data

*Hash Indices

The records are stored in buckets.

• Bucket is a unit of storage containing records (a bucket is a disk block).
• Bucket can be obtained from search key using hash function.

Def. Hash function \(h\)

• A function from search key \(K\) to bucket address.
• Entries with different search keys mapped to the same bucket.
• The entire bucket searched sequentially to locate an entry.

Def. Hash Index Buckets store entries with pointers to records.

Def. Hash File Organization Buckets store records of the hash file. The process of obtaining the bucket of a record from search key using hashing function.

Def. Static Hashing Hash function \(h\) cannot be modified.

Def. Dynamic Hashing Hash function \(h\) can be modified dynamically.

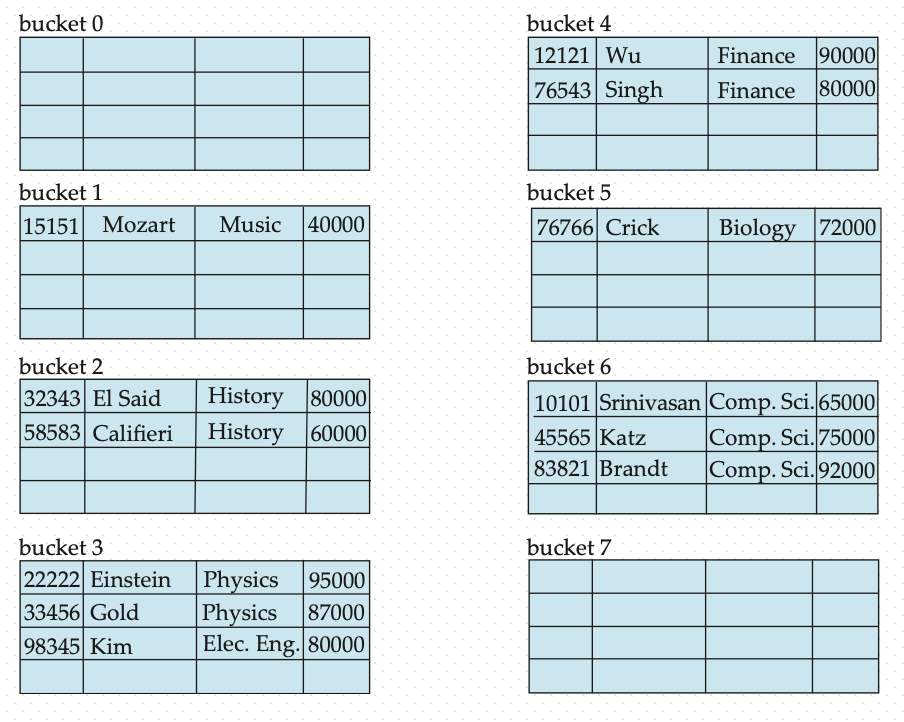
Example of hash file organization

Hash the instructor file, using dept_name as key. There are \(10\) buckets. The binary representation of the \(i\) character is the integer \(i\). The hash function returns the sum of the binary representations of the characters modulo \(10\)

hash file organization example

Figure 2: Possible buckets

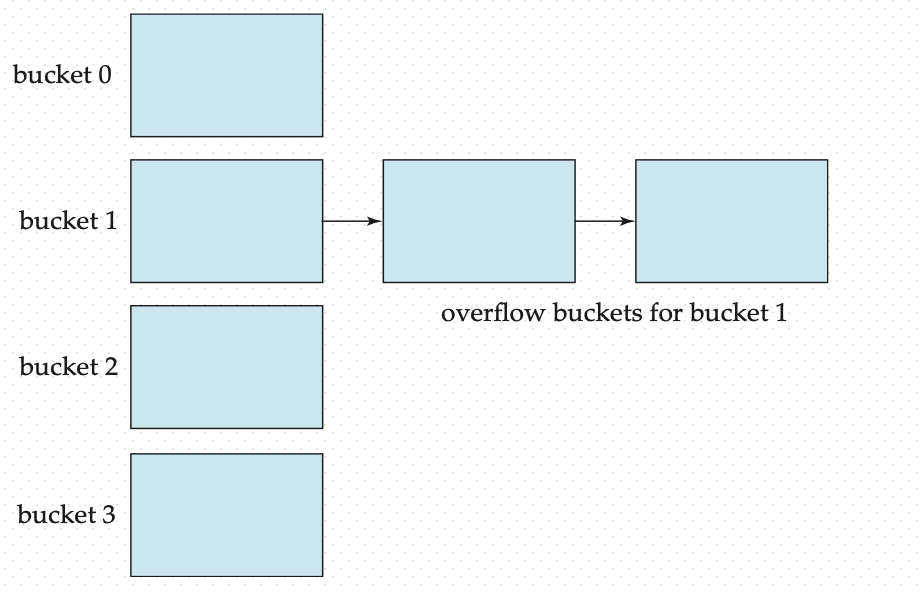
Bucket Overflows

Def. Bucket Overflow It occurs because of

• Insufficient buckets.
• Non-uniform distribution of records due to:
  • Multiple records have same search key value.
  • Hash function produces non-uniform distribution of the key values.

The probability of bucket overflow can be reduced, but cannot be eliminated; It is handled by using overflow buckets.

Def. Overflow Chaining The overflow buckets of a given bucket are chained together.

overflow chaining

Figure 3: Overflow chaining

Multiple-Key Access

Def. Composite Search Keys. Composite search keys are search keys containing more than one attribute. e.g.

CREATE INDEX index_name ON table_name(column1, column2, ...);

Def. Lexicographic Ordering. \((a_1, a_2) < (b_1, b_2)\) if either \(a_1 < b_1\) or \(a_1 = b_1\) and \(a_2 < b_2\).

复合索引左前缀原则

Suppose we have an index on composite search keys (dept_name, salary) with the where clause where dept_name = "Finance" and salary = 8000;. Index on (dept_name, salary) to fetch records with both conditions.

• Can also efficiently handle where dept_name = "Finance" and salary < 8000;
• Can also efficiently handle where dept_name = "Finance";

But cannot efficiently handle

1. where dept_name < "Finance" and salary = 8000;. May fetch many records that satisfy the first but not the second condition.
2. where salary = 8000;. The index is not used for query.

查询条件必须包含复合索引的前缀列，索引才能被高效利用。

Creation of Indices

• Indices on primary key created automatically.
• Indices can speed up lookups, but impose cost on updates.

Def. Index Definition in SQL

CREATE INDEX <index-name> on <relation-name>(<attributes-list>);

DROP INDEX <index-name>;

Use CREATE UNIQUE INDEX to indirectly specify and enforce the condition that the search key is a candidate key.

We can enforce DB to use index.

SELECT * FROM tbMROData WITH (INDEX = timeide) WHERE ...

Also we can enforce not.

ALTER INDEX timeide on tbMRODatanew
DISABLE
SELECT * FROM tbMRODatanew WHERE ...

我们应该在哪些属性上建立索引，可以从以下几个角度分析。

1. 对 SELECT 查询，针对 SELECT，FROM，WHERE，GROUPBY，HAVING 操作，在以下属性上建立聚集或非聚集索引，有利于提高访问速度。

   • WHERE 子句涉及到的查询属性，连接属性。
   • GROUPBY 子句中的分组属性。

2. 对 DELETE，FROM，WHERE 操作，如果在 WHERE 查询条件属性上建立索引，有利于在数据库文件中快速定位由 WHERE 条件定义的需要删除的元组。但删除这些元组后，将引起 DBMS 对索引进行调整重组，引起额外的系统开销，可能会降低 DELETE 的执行速度。

3. 对 INSERT 操作，在关系表中插入新元组后，DBMS 将根据新插入的元组在索引属性上的值，对表中的索引进行调整重组，必然引起额外系统开销，降低 INSERT 的执行速度。

4. 对 UPDATE，SET，WHERE 操作，如果在 WHERE 查询条件属性上建立了索引，有利于在数据库文件中快速定位 UPDATE 需要访问的元组。但如果 SET 操作修改了索引涉及到的属性的值，则会引发 DBMS 对索引的重组。索引重组带来额外的系统开销，降低了 UPDATE 的执行速度。

例题

Consider the following tables:

• factory(factoryID, name, manager, account)
• employee(employeeID, name, age, factoryID)
• airconditioner(serialID, date, model, price, factoryID)

1. Consider the following SQL query. In addition to the primary indices on the primary keys of the tables, on which attributes in the tables the indices can be further defined to speed up the query?

SELECT A.factoryID, AVG(employeeID)
FROM factory AS A, employee AS B
WHERE A.factoryID = B.factoryID AND age > 20 AND account > 30000
GROUP BY B.factoryID;

factoryID, age in employee, account in factory.

(2). For the following query, a non-clustered index is defined on the attribute model. Does this index speed up or slow down the operation, and why?

UPDATE airconditioner
SET price = price + 100
WHERE model = 'GL2020';

This index will speed up the operation. Because DBMS can seek tuples in UPDATE and modify SET based on this index. What’s more, there is no necessary to modify this index.

(3). For the following delete operation, a primary index has been defined on the primary key serialID. Does this index speed up or slow down the operation, and why?

DELETE
FROM airconditioner
WHERE model = 'HX8302' AND price > 1500;

The delete operation will slow down.

This is because, when searching for the target tuples to be deleted based on the WHERE condition (involving the two attributes model and price), the primary index defined on the primary key serialID cannot be utilized. Moreover, after deleting the target tuples that satisfy the WHERE condition, the DBMS needs to spend additional time readjusting the primary index defined on serialID.

Therefore, overall, the primary index on serialID reduces the speed of the delete operation.

4. If a multiple-attribute index is defined on airconditioner by CREATE INDEX DMFIndex ON airconditioner(date, model, factoryID);, can the index DMFIndex speed up the following queries? why?

(i).

SELECT serialID
FROM airconditioner
WHERE date = '2021-11-30' AND model = 'Haier';

The WHERE condition uses two attributes of DMFIndex and satisfies the left-prefix principle, so the index takes effect and can speed up the query.

(ii).

SELECT serialID
FROM airconditioner
WHERE date = '2021-11-30' AND price > 2000;

The WHERE condition uses one attribute of DMFIndex, date, and satisfies the left-prefix principle, so the index takes effect and can speed up the query.

(iii).

SELECT serialID
FROM airconditioner
WHERE date = '2021-11-30' AND factoryID = '1040';

The WHERE condition uses two attributes of the DMFIndex: date and factoryID. From the perspective of the left-prefix requirement, only the query condition date = '2021-11-30' can utilize the index, and the index can partially accelerate the query.

(iv).

SELECT serialID
FROM airconditioner
WHERE model = 'Haier' AND factoryID = '1040';

The WHERE condition uses two attributes of the DMFIndex: model and factoryID, but it does not satisfy the left-prefix rule. Therefore, the index is ineffective and cannot accelerate the query.

Appendix

访问方式

1. 聚集索引查找
2. 聚集索引扫描

seek and scan

Figure 4: 聚集索引树的查找和扫描