Chapter 2: Relation Model
Some important definition: relation schema, relation instance, super key, candidate key, primary key, foreign key, schema diagram (different from ER diagram in chapter 6), algebra expression.
Structure of Relational Databases
Def. A relational database consists of a collection of tables
| ID | name | dept_name | salary |
|---|---|---|---|
| 10101 | Srinivasan | Comp. Sci. | 65000 |
| 12121 | Wu | Finance | 90000 |
| … | … | … | … |
Def.
- \(R = (A_1, A_2, \cdots, A_n)\) is a relation schema, \(A_i\) is attribute, \(D_i\) is domain of \(A_i\).
- The domain of the attribute is the set of allowed values
- Attribute values are (normally) required to be atomic, indivisible.
- The special value null is a member of every domain, indicating that the value is unknown.
- The null values causes complications in definition of operations, e.g. indexing failure.
- A relation instance \(r\) is defined over schema \(R\), denoted by \(r(R)\)
- The current values \(r(R)\) are specified by a table.
- An element \(t\) of relation \(r\) is called a tuple, denoted by a row in table.
Relations are unordered. Ordered of tuples is irrelevant. Tuples may be stored in an arbitrary order. Attributes orders are also irrelevant.
A relation instance \(r(R)\) may not include the whole table of \(R\).
Database Schema
Def. Database schema is the logical structure of database.
Def. Database instance is a snapshot of data in database at a given instant in time.
Example:
- Schema: instructor (ID, name, dept_name, salary)
- Instance:
| ID | name | dept_name | salary |
|---|---|---|---|
| 22222 | Einstein | Physics | 95000 |
| 12121 | Wu | Finance | 90000 |
| 32343 | El Said | History | 60000 |
| 45565 | Katz | Comp. Sci. | 75000 |
| 98345 | Kim | Elec. Eng. | 80000 |
| 76766 | Crick | Biology | 72000 |
| 10101 | Srinivasan | Comp. Sci. | 65000 |
Keys
Def. Super key is a set of one or more attributes that can be used to identify uniquely a tuple in the relation.
Def. Given relation schema \(R = (A_1, A_2, \cdots, A_n)\), a subset \(K\) is super key if no two distinct tuples have the same values on all attributes in \(K\).
The super key may contain redundant attributes, e.g. {ID} and {ID, name, dept_name}.
Def. \(K\) is a candidate key if \(K\) is minimal super key, e.g. {ID}.
Def. Primary key is a candidate key (one of candidate keys) as principal means to identify tuples.
Def. Integrity of primary key requires values on the primary key are not permitted to be null.
Def. Primary attributes are the attributes that appear in at least one candidate key.
Note: It is recommended to select numeric (int, float) candidate keys as the primary key to improve query performance based on the primary key. Avoid selecting string-type attributes, such as varchar or datetime (e.g. student_name).
Def. Foreign Key
If \(X\) is one or more attributes in schema \(r_1\), e.g. instructor, and \(X\) is also the primary key of another schema \(r_2\), e.g. department.
- \(X\) is called a foreign key from \(r_1\) referencing \(r_2\).
- \(r_1\) is called the referencing relation of the foreign key dependency.
- \(r_2\) is called the referenced relation of the foreign key
Note: There are foreign key relationships between database tables. When importing data, first import the data of the referenced relation \(r_2\) (e.g., department), and then import the data of the referencing relation \(r_1\) (e.g., instructor).
Def. Referential Integrity
Values appearing in foreign key attributes of any tuples in the referencing relation \(r_1\) (instructor) must appear in attributes of at least one tuples in the referenced relation \(r_2\) (department).
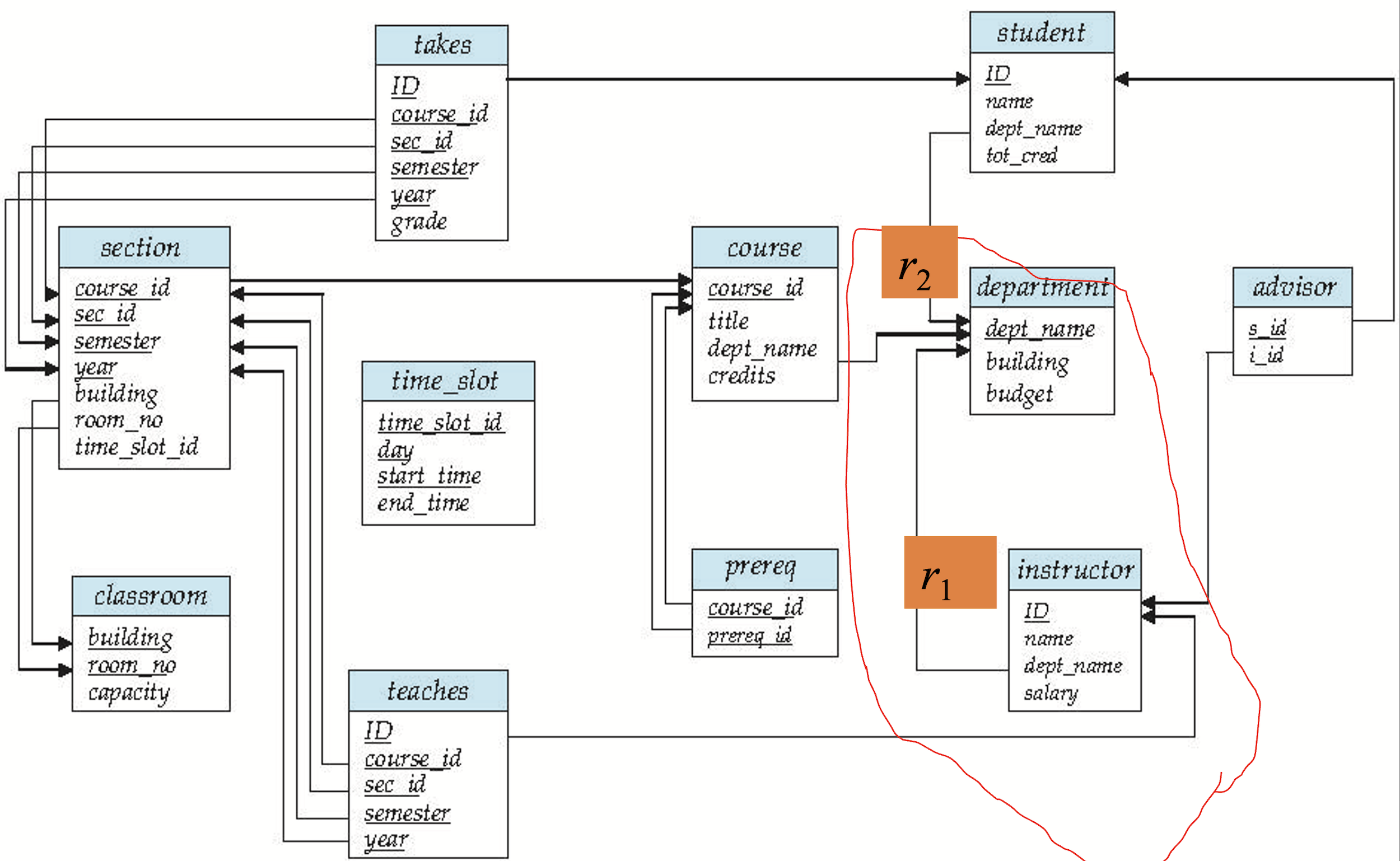
Schema Diagram for University Database
A database schema, with primary key and foreign key dependency, can be depicted as schema diagram.
- Nodes: schema, attributes, primary key
- Arcs: foreign key dependency, from referencing relation \(r_1\) to referenced relation \(r_2\)
Relational Algebra Expression
Def. Relation algebra expression is defined as follows
- A basic expression is a relation \(r\) in DB, or a constant relation \(C = \{r_1, r_2, \cdots, r_n\}\), written by listing its tuples.
- A general expression is defined: if \(E_1\) and \(E_2\) are relational algebra expressions, we have
- \(E_1 \cup E_2\)
- \(E_1 - E_2\)
- \(E_1 \times E_2\)
- \(\sigma_{p} (E_1)\)
- \(\Pi_{s} (E_1)\)
- \(\rho_{X} (E_1)\)
Select Operation
Def. The select operation selects tuples that satisfy a given predicate.
- Notation: \(\sigma_{p} (r)\). \(p\) is called the selection predicate
- Example: select those tuples of the instructor relation where the instructor is in Physics department
- Query: \(\sigma_{\text{dept\_name} = \text{"Physics"}} (\text{instructor})\)
What’s more, we allow comparisons (\(=\), \(\neq\), \(>\), \(\geq\), \(<\), \(\leq\)) in the selection predicate and can combine several predicates into a larger predicate by using connectives: \(\land\), \(\lor\), \(\lnot\). For example, find the instructors in Physics with salary greater \(90000\): \(\sigma_{\text{dept\_name} = \text{"Physics"} \land \text{salary} > 90000} (\text{instructor})\).
The select predicate may include comparisons between two attributes. For example, find all departments whose name is the same as their building name: \(\sigma_{\text{dept\_name} = \text{building}} (\text{department})\).
Project Operation
Def. Operation that returns its argument relation, with certain attributes left out.
- Notation: \(\Pi_{A_1, A_2, \cdots, A_{k}} (r)\)
- The result defined as \(k\) columns by erasing the columns that are not listed.
- Example: eliminate the dept_name attribute of instructor
- Query: \(\Pi_{\text{attributes except dept\_name}} (\text{instructor})\)
Composition of relational operations. For example, find the names of all instructors in Physics department: \(\Pi_{\text{name}} (\sigma_{\text{dept\_name} = \text{"Physics"}} (\text{instructor}))\)
Join Operation
Def. Cartesian product operation (denoted by \(\times\)) allows to combine information from two relations. For example, Cartesian product of instructor and teaches is written as: \(\text{instructor} \times \text{teaches}\).
Cartesian product, we suppose \(A = \{a, b, c\}\), \(B = \{d, e, f\}\), \(A \times B = \{ad, ae, af, bd, be, bf, cd, ce, cd\}\).
Def. The join operation combine select operation and Cartesian product operation into a single operation.
Consider relation instance \(r(R)\) and \(s(S)\). Let \(\theta\) be a predicate on attributes in schema \(R\) union \(S\). The join operation is defined as follows: \(r \Join_{\theta} s = \sigma_{\theta} (r \times s)\) (will be used in chapter 16).
Union Operation
The union operation allows us to combine two relations. Notation: \(r \cup s\). For \(r \cup s\) to be valid.
- \(r\), \(s\) must have the same arity (same number of attributes)
- The attribute domains must be compatible
For example, find all courses taught in the Fall 2017 semester, or in the Spring 2018 semester, or in both: \(\Pi_{\text{course\_id}}(\sigma_{\text{semester} = \text{"Fall"} \land \text{year} = 2017}(\text{section})) \cup \Pi_{\text{course\_id}}(\sigma_{\text{semester} = \text{"Spring"} \land \text{year} = 2018}(\text{section}))\)
Set Intersection Operation
Def. The set intersection operation allows us to find tuples that are in both input relations. Notation: \(r \cap s\). Similar to union operation.
Set Difference Operation
Def. The set difference operation allows find tuples that are in one relation but are not in another. Notation: \(r - s\).
The Assignment Operation
Def. The assignment operation is denoted by \(\leftarrow\). Working like assignment in programming language. For example, find all instructor in Physics and Music department.
\[ \begin{aligned} \text{Physics} &\leftarrow \sigma_{\text{dept\_name} = \text{"Physics"}} (\text{instructor}) \\ \text{Music} &\leftarrow \sigma_{\text{dept\_name} = \text{"Music"}} (\text{instructor}) \\ \text{Physic} &\cup \text{Music} \end{aligned} \]
The Rename Operation
Def. The results of relational algebra expression do not have a name. The rename operation \(\rho\) is provided for a name. The expression \(\rho_{X}(E)\) returns the result of express \(E\) under the name \(X\).
Equivalent Queries
The two queries are not identical, however they give the same result on any database.
We can use different queries to improve querying. (chapter 16)