条件随机场

Only focus on tagging problem and linear chain

Probabilistic Undirected Graphical Model

Pairwise Markov Property

Node $u$, $v$, and all nodes $O$. Their corresponding random variable are $Y_u$, $Y_v$, $Y_O$($Y$ means random variable). They have following probabilistic relationship.

$$P(Y_u, Y_v | Y_O) = P(Y_u | Y_O) P(Y_v | Y_O) \tag{1}$$

Local Markov Property

Node $v$, $W$ is all nodes adjacent to $v$, and $O$ is remaining nodes. They have following probabilistic relationship.

$$P(Y_v, Y_O | Y_W) = P(Y_v | Y_W) P(Y_O | Y_W) \tag{2}$$

Global Markov Property

Nodes set $A$, $B$, $C$. $A$ and $B$ are divided by $C$. They have following probabilistic relationship.

$$P(Y_A, Y_B | Y_C) = P(Y_A | Y_C) P(Y_B | Y_C) \tag{3}$$

Definition: Probabilistic Undirected Graphical Model

Satisfying three Markov properties.

Definition: Clique and Maximum Clique

clique: A subnet with all nodes adjacent to other nodes.
maximum clique: The biggest subnet with all nodes adjacent to other nodes.

Factorization

$$\begin{align} P(Y) &= \frac{1}{Z} \prod_{C} \psi_{C}(Y_C), C \text{ is a maximum clique} \tag{4} \\ Z &= \sum_{Y} \prod_{C} \psi_{C}(Y_C), Z \text{ is normalization factor} \tag{5} \\ \psi_{C}(Y_C) &= \exp\{-E(Y_C) \} \tag{6} \end{align}$$

---

CRF

Definition: Linear Chain conditional Random Field

We suppose that $X$ and $Y$ are random variable. If random $Y$ is a Markov random field, that is

$$P(Y_v | X, W_w, w \neq v) = P(Y_v | X, Y_w, w \sim v) \tag{7}$$

$w \sim v$ means $v$ is adjacent to $w$.

Normally, we consider $X$ has the same structure as $Y$.

Linear Chain CRF

Figure 1: Example for linear chain

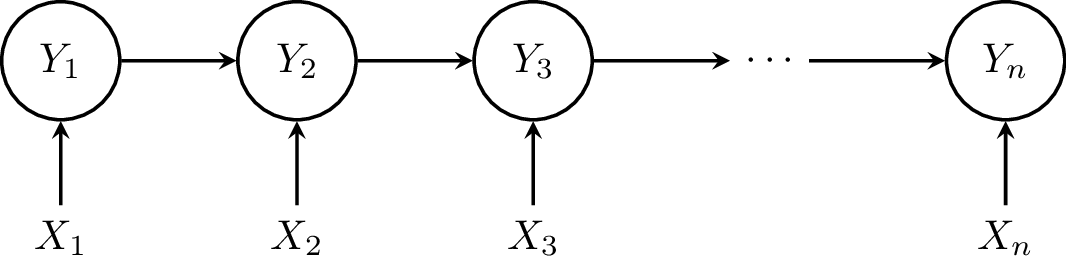
We have following probabilistic relationship.

$$P(Y_i | X, Y_1, \dots, Y_{i-1}, Y_{i+1}, \dots, Y_n) = P(Y_i | X, Y_{i - 1}, Y_{i + 1}) \tag{8}$$

Parametric form of linear-chain Conditional Random Fields

$$P(y | x) = \frac{1}{Z(x)} exp\left(\sum_{i,k}\lambda_k t_k(y_{i -1}, y_i, x, i) + \sum_{i,l}\mu_l s_l(y_i, x, i))\right) \tag{9}$$

Of which

$$Z(x) = \sum_{y} exp\left(\sum_{i,k}\lambda_k t_k(y_{i -1}, y_i, x, i) + \sum_{i,l}\mu_l s_l(y_i, x, i)\right) \tag{10}$$

Among them, $t_k$ and $s_l$ are feature function, $\lambda_k$ and $\mu_l$ are corresponding weights.

Simplification

$$f_k(y_{i-1},y_i,x,i) = \begin{cases} t_k(y_{i-1}, y_i, x, i), \quad &k = 1,2, \dots,K_1 \tag{11} \\\\ s_l(y_i,x,i), \quad &k = K_1 + 1; \text{ } l = 1,2,\dots, K_2 \end{cases}$$ $$f_k(y, x) = \sum_{i=1}^{n} f_k(y_{i-1},y_i,x,i), \quad k = 1,2,\dots,K \tag{12}$$ $$w_k = \begin{cases} \lambda_k, &k = 1,2,\dots,K_1 \\\\ \mu_i, &k = K_1 + l; \text{ } l = 1, 2, \dots, K_2 \tag{13} \end{cases}$$

So

$$\begin{align*} P(y|x) &= \frac{1}{Z(x)}exp\sum_{k=1}^{K}w_kf_k(y,x) \tag{14} \\ Z(x) &= \sum_{y} exp\sum_{k=1}^{K} w_kf_k(y,x) \tag{15} \end{align*}$$

That is

$$\begin{align} P_w(y|x) = \frac{exp(\vec{w} \cdot \vec{F}(y,x))}{Z_w(x)} \tag{16} \end{align}$$ $$Z_w(x) = \sum_{y}exp(\vec{w} \cdot \vec{F}(y,x)) \tag{17}$$

Matrix Form

For each label sequence, we introduce special start point and end point labels, $y_0 = \text{start}$ and $y_{n+1} = \text{stop}$. For each position in observation sequence $x$ $i =1,2,\dots,n+1$, we can define a matrix $m \in \mathbb{R}^m$

$$\begin{align} M_i(x) &= [M_i(y_{i-1}, y_i | x)] \tag{18} \\ M_i(y_{i-1}, y_i |x) &= exp \left(W_i(y_{i-1} y_i | x\right) \tag{19} \\ W_i(y_{i-1}, y_i |x) &= \sum_{k=1}^{K}w_kf_k(y_{i-1},y_i,x,i) \tag{20} \end{align}$$

So

$$P_w(y|x) = \frac{1}{Z_w(x)} \prod_{i=1}^{n+1} M_i(y_i,y_i|x) \tag{21}$$

Specially

$$Z_w(x) = [M_1(x)M_2(x) \dots M_{n+1}(x)]_{start,stop} \tag{22}$$

---

Calculation

Forward-Backward Algorithm

For each index $i = 0, 1, \dots, n + 1$, we define forward vector $\alpha_i(x)$;

$$\alpha_0(y|x) = \begin{cases} 1, &y = start \\ 0, &otherwise \tag{23} \end{cases}$$

recursive formula is

$$\alpha_i^T(y_i|x) = \alpha_{i-1}^T (y_{i-1}|x) [M_i(y_{i-1},y_i|x)],\quad i = 1,2,\dots,n+1 \tag{24}$$

also, we define backward vector;

$$\begin{align} \beta_{n+1}(y_{n+1}|x) &= \begin{cases} 1, &y_{n+1} = stop \\ 0, &otherwise \tag{25} \end{cases} \\ \beta_i(y_i|x)& = [M_{i+1}(y_i,y_{i+1}|x)] \beta_{i+1}(y_{i+1}|x) \tag{26} \end{align}$$

Probabilistic Calculation

$$P(Y_i = y_i | x) = \frac{\alpha_i^T(y_i | x) \beta_i(y_i | x)}{Z(x)} \tag{27}$$ $$P(Y_{i-1} = y_{i-1}, Y_i = y_i |x) = \frac{\alpha_{i-1}^T(y_{i-1} |x) M_i(y_{i-1},y_i | x) \beta_i(y_i | x)}{Z(x)} \tag{28}$$

of which

$$Z(x) = \alpha_n^T(x)\mathbf{1} = \mathbf{1} \beta_1(x)$$

---

Learning Algorithm

Improved Iterative Scaling