The Network Layer

Notice !: Computer Networking_ A Top-Down Approach, Global Edition, 3th Edition

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
N = {u};
for (auto a : nodes) {
    if (isAdjacent(u, a)) {
      D[a] = Cost(u, a);
      P[a] = u;
    }
    else {
      D[a] = INF;
      P[a] = a;
      }
}
while (! all nodes in N) {
    D[a] = min(D)
    for (auto b : nodes) {
        if (isAdjacent(b ,a)) {
          D[b] = min(D[b], Cost(b, a) + D[a])
          if (D[b] == Cost(b, a) + D[a]) P[b] = a;
        }
    }
}

End-of-chapter exercises

Chapter 4

P.6

Questions:

In the text we have used the term connection-oriented service to describe a transport-layer service and connection service for a network-layer service. Why the subtle shades in terminology?

Answer:

The subtle difference in terminology reflects the distinct roles and responsibilities of the transport and network layers:

  • Connection-oriented service (Transport Layer):
    At the transport layer, a connection-oriented service (such as TCP) establishes, maintains, and terminates a logical end-to-end connection. This connection is defined between two processes on the end hosts (e.g., two TCP sockets). This service ensures reliable, ordered, and error-checked delivery of data across the entire network path, directly between the communicating applications.

  • Connection service (Network Layer):
    At the network layer, a connection service (such as a virtual circuit) refers to the establishment of a logical path through the network, typically between routers or switches. This connection is defined between two hosts (and their intervening routers in the case of virtual-circuit networks). This path helps guide packets from source to destination but does not necessarily guarantee reliability or ordering. The focus here is on the route and forwarding of packets within the network infrastructure.

In summary:
The term “connection-oriented service” at the transport layer emphasizes end-to-end reliability and communication, while “connection service” at the network layer highlights the setup of a path through the network, without necessarily providing full end-to-end guarantees. The nuanced terminology helps clarify the different scopes and guarantees provided by each layer.

P.9

Consider a datagram network using 32-bit host addresses. Suppose a router has four links, numbered 0 through 3, and packets are to be forwarded to the link interfaces as follows:

Destination Address Range Link Interface
11100000 00000000 00000000 00000000
through
11100000 00111111 11111111 11111111
 0
11100000 01000000 00000000 00000000
through
11100000 01000000 11111111 11111111
 1
11100000 01000001 00000000 00000000
through
11100001 01111111 11111111 11111111
 2
otherwise
 3

Questions:

a. Provide a forwarding table that has four entries, uses longest prefix matching, and forwards packets to the correct link interfaces.

b. Describe how your forwarding table determines the appropriate link interface for datagrams with destination addresses:

11001000 10010001 01010001 01010101
11100001 01000000 11000011 00111100
11100001 10000000 00010001 01110111

Answer:

a. Forwarding Table with Longest Prefix Matching

Header Link Interface(output)
11100000 00 0
11100000 01000000 1
1110000 2
otherwise 3

Explanation:

  • Each entry uses the longest prefix that matches the given address range.
  • The router checks the destination address against each prefix, starting from the longest, and forwards the packet to the corresponding interface.

b. Determining the Link Interface for Given Addresses

  1. 11001000 10010001 01010001 01010101

    • This address does not match any of the specified prefixes (does not start with 111…), so it is forwarded to interface 3.

  2. 11100001 01000000 11000011 00111100

    • This address matches the third entry:
      • Prefix: **1110000**1 01000001 00000000 00000000
      • So, it is forwarded to interface 2.

  3. 11100001 10000000 00010001 01110111

    • This address matches the third entry:
      • Prefix: **1110000**1 10000000 00010001 01110111
      • So, it is forwarded to interface 2.

P.10

Consider a datagram network using 8-bit host addresses. Suppose a router uses longest-prefix matching and has the following forwarding table:

Prefix Match Interface
00 0
010 1
011 2
10 2
11 3

Questions:

For each of the four interfaces, give the associated range of destination host addresses and the number of addresses in the range.

Answer:

Interface Destination Address Range Number of Addresses
0 00000000 - 00111111 64
1 01000000 - 01011111 32
2 01100000 - 01111111
10000000 - 10111111		 96
3 11000000 - 11111111 64

P.17

Question:

Consider sending a 2400-byte datagram into a link that has an MTU of 700 bytes. Suppose the original datagram is stamped with the identification number 422. How many fragments are generated? What are the values in the various fields in the IP datagram(s) generated related to fragmentation?

Answer:

According to IPv4 datagram format, each fragment includes a 20-bytes header. So we need $\lceil\frac{2400 - 20}{700 - 20}\rceil = 4 $ fragments. Each fragment has the same Version, Header length, Type of service, and so on. What makes them different is as follows:.

Fragment Datagram length Offset Flag
1 700 0 1
2 700 85 1
3 700 170 1
4 380 255 0

P.18

Question:

Suppose datagrams are limited to 1,500 bytes (including header) between source Host A and destination Host B. Assuming a 20-byte IP header, how many datagrams would be required to send an MP3 consisting of 5 million bytes? Explain how you computed your answer.

Answer:

We need $\lceil\frac{5000000}{1500 - 20}\rceil = 3379$ datagrams.

P.19

Consider the network setup in Figure 4.22. Suppose that the ISP instead assigns the router the address 24.34.112.235 and that the network address of the home network is 192.168.1/24.

Question:

a. Assign addresses to all interfaces in the home network.

b. Suppose each host has two ongoing TCP connections, all to port 80 at host 128.119.40.86. Provide the six corresponding entries in the NAT translation table.

Answer:

a. Address assignments for interfaces in the home network:

According to Figure 4.22 and the given information.

  • Router WAN side address is 24.34.112.235.
  • Router LAN side 192.168.1.4
  • Host 1 address is 192.168.1.1
  • Host 2 address is 192.168.1.2
  • Host 3 address is 192.168.1.3

b. NAT translation table entries

WAN side LAN side
24.34.112.235, 50001 192.168.1.1, 3345
24.34.112.235, 50002 192.168.1.1, 3346
24.34.112.235, 50003 192.168.1.2, 3345
24.34.112.235, 50004 192.168.1.2, 3346
24.34.112.235, 50005 192.168.1.3, 3345
24.34.112.235, 50006 192.168.1.3, 3346

P.24

Figure P.24: Example network for dijkstra algorithm

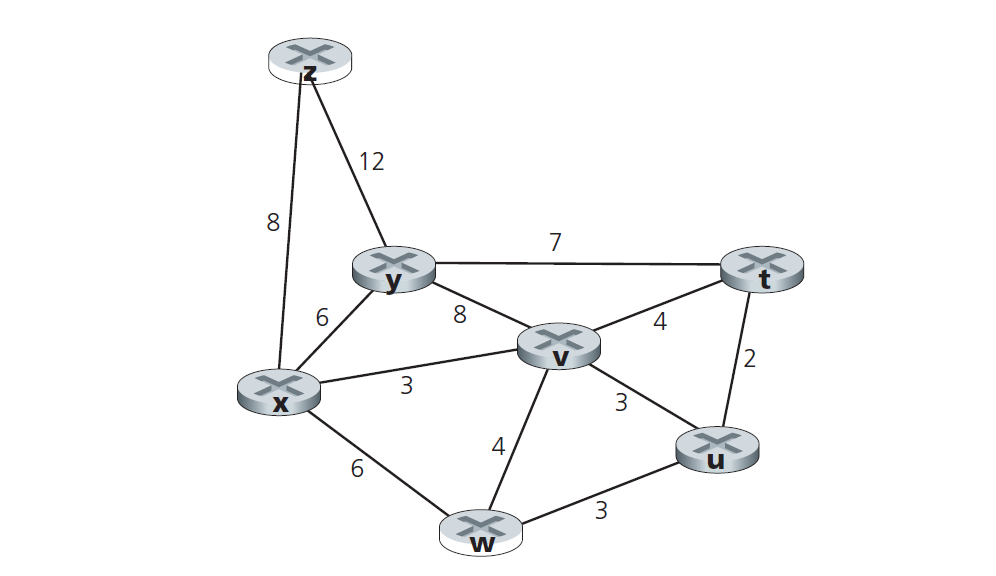
Question:

Consider the following network. With the indicated link costs, use Dijkstra’s shortest-path algorithm to compute the shortest path from x to all network nodes. Show how the algorithm works by computing a table similar to Table 4.3.

Answer:

$N’ = \\{x\\}$

step $D(x)$ $P(x)$ $D(y)$ $P(y)$ $D(z)$ $P(z)$ $D(v)$ $P(v)$ $D(u)$ $P(u)$ $D(w)$ $P(w)$ $D(t)$ $P(t)$ $N’$
0 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $\infty$ $6$ $x$ $\infty$ $x$
1 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $x$ $7$ $v$ $xv$
2 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $x$ $7$ $v$ $xvy$
3 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $w$ $7$ $v$ $xvyu$
4 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $x$ $7$ $v$ $xvyuw$
5 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $x$ $7$ $v$ $xvyuwt$
6 $0$ $x$ $6$ $x$ $8$ $x$ $3$ $x$ $6$ $v$ $6$ $x$ $7$ $v$ $xvyuwtz$

So the shortest path from $x$ to all nodes is follow.

Destination Shortest Distance Path
$x$ $0$ $x$
$v$ $3$ $x \to v$
$y$ $6$ $x \to y$
$w$ $6$ $x \to w$
$u$ $6$ $x \to v \to u$
$t$ $7$ $x \to v \to t$
$z$ $8$ $x \to z$

P.26

Figure P.26: Example network for distance-vector algorithm

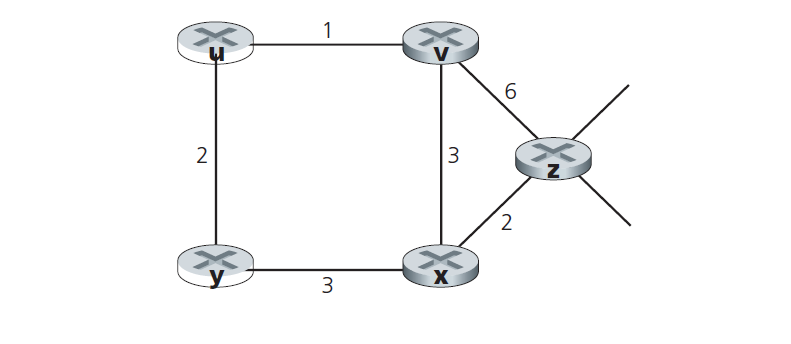
Question:

Consider the network shown below, and assume that each node initially knows the costs to each of its neighbors. Consider the distance-vector algorithm and show the distance table entries at node z.

Answer:

Node z table:

First round

cost to
x y z u v
from x $\infty$ $\infty$ $\infty$ $\infty$ $\infty$
from y $\infty$ $\infty$ $\infty$ $\infty$ $\infty$
from z 2 $\infty$ 0 $\infty$ 6
from u $\infty$ $\infty$ $\infty$ $\infty$ $\infty$
from v $\infty$ $\infty$ $\infty$ $\infty$ $\infty$

Second round

cost to
x y z u v
from x 2 3 $\infty$ $\infty$ 3
from y 3 $\infty$ $\infty$ 2 $\infty$
from z 2 5 0 7 5
from u $\infty$ 2 $\infty$ $\infty$ 2
from v 3 $\infty$ 6 1 $\infty$

Because the question only asks to show the distance table entries at node z, we do not need to compute the full routing tables for all nodes. The Second round result about node z is also the finial result.

Computer Network > Network Layer
#Network Layer #Control Plane #Routing #Networking
The Network Layer
http://example.com/2025/05/30/The-Network-Layer/
作者
ddccffq
发布于
2025年5月30日
许可协议