支持向量机

Linear SVM in Linearly Separable Case

Define Training Data

$$T = \\{(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)\\}$$ $$x_i \in \mathcal{X} = \mathbb{R}^n, \quad y_i \in \mathcal{Y} = \{+1, -1\}, \quad i = 1, 2, \ldots, N$$

Define Separating Hyperplane

$$w^* \cdot x + b^* = 0$$

Define Classification Decision Function

$$f(x) = \operatorname{sign}(w^* \cdot x + b^*)$$

Define Functional Margin

$$\hat{\gamma}_i = y_i (w \cdot x_i + b)$$ $$\hat{\gamma} = \min_{i = 1, 2, \ldots, N} \hat{\gamma}_i$$

Define Geometric Margin

$$\gamma_i = y_i \times \left(\frac{w \cdot x_i + b}{\lVert w \rVert}\right)$$

$\lVert w \rVert$ is $L_2$ norm

$$\gamma = \min_{i=1, \ldots, N} \gamma_i$$

What’s More

$$\gamma_i = \frac{\hat{\gamma}_i}{\lVert w \rVert}$$

Maximize Margin
Originally, we solve the following question.

$$\max_{w, b} \quad \gamma$$ $$s.t. \quad y_i\left(\frac{w}{\lVert w \rVert} \cdot x_i + \frac{b}{\lVert w \rVert}\right) \geq \gamma, \quad i = 1, 2, \ldots ,N$$

We can transform this into a convex quadratic programming problem.

$$\min_{w, b} \quad \frac{1}{2} \lVert w \rVert ^2$$ $$s.t. \quad y_i(w \cdot x_i + b) - 1 \geq 0, \quad i = 1, 2, \ldots, N$$

Support Vector

$$y_i(w \cdot x_i + b) - 1 = 0$$

Margin

$$d = \frac{2}{\lVert w \rVert}$$

Learning Algorithm

• input: $T$

• output: Separating Hyperplane and $f(x)$

• Solve and get the optimal solution $\alpha^*$.

  $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i$$

$$s.t. \quad \sum_{i = 1}^{N} \alpha_i y_i = 0, \quad \alpha_i \geq 0, \quad i = 1, 2, \ldots, N$$ $$\alpha^* = (\alpha_1^{\ast}, \alpha_2^{\ast}, \ldots, \alpha_N^{\ast})$$

• Calculate.

$$w^{\ast} = \sum_{i=1}^{N} \alpha_i^{\ast} y_i x_i$$ $$\forall y_j > 0, \quad b^\ast = y_j - \sum_{i=1}^{N}\alpha_i^\ast y_i(x_i \cdot x_j)$$

Linear SVM

$$y_i (w \cdot x_i + b) \geq 1 - \xi_i$$ $$\min_{w, b, \xi} \quad \frac{1}{2} \lVert w \rVert^2 + C \sum_{i = 1}^{N} \xi_i$$ $$s.t. \quad y_i(w \cdot x_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \ldots, N, \quad \xi_i \geq 0$$

Learning Algorithm

• input: $T$

• output: Separating Hyperplane and $f(x)$

• Solve and get the optimal solution $\alpha^*$.

  $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i$$

$$s.t. \quad \sum_{i = 1}^{N} \alpha_i y_i = 0, \quad C \geq \alpha_i \geq 0, \quad i = 1, 2, \ldots, N$$ $$\alpha^* = (\alpha_1^{\ast}, \alpha_2^{\ast}, \ldots, \alpha_N^{\ast})$$

• Calculate.

$$w^{\ast} = \sum_{i=1}^{N} \alpha_j^{\ast} y_i x_i$$ $$\forall C > \alpha_j^{\ast} > 0, \quad b^\ast = y_j - \sum_{i=1}^{N}\alpha_i^\ast y_i(x_i \cdot x_j)$$

Hinge Loss Functional

$$\min_{w, b} \quad \sum_{i = 1}^{N} [1 - y_i(w \cdot x_i + b)]_+ + \lambda \lVert w \rVert^2$$

Non-linear SVM

Kernel Trick

Figure 1: Example for kernel trick

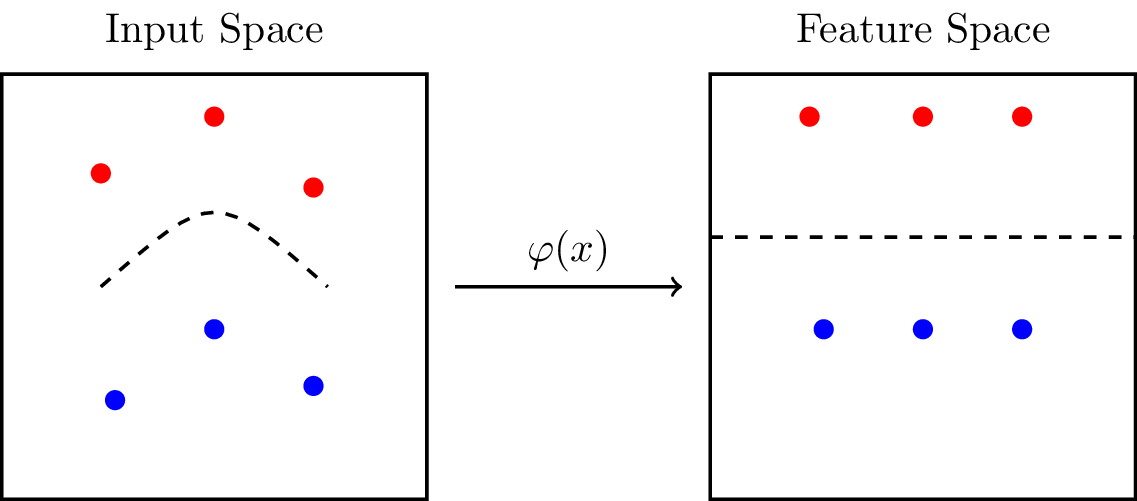
Positive Definite Kernel Function

$K :\mathcal{X} \times \mathcal{X} \to \mathbb{R}$ is a symmetric function, $K(x, z)$ is positive definite kernel function $\Leftrightarrow$ $\forall x_i \in \mathcal{X}, \quad i = 1, 2, 3, \dots, m, \quad \text{the gram matrix corresponding ot } K(x, z) \text{is positive semi-definite.}$

Gram Matrix

$$K = [K(x_i, x_j)]_{m \times m} \tag{1}$$

Learning Algorithm

• input: $T$

• output: Separating Hyperplane and $f(x)$

• Solve and get the optimal solution $\alpha^*$.

  $$\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i$$

$$s.t. \quad \sum_{i = 1}^{N} \alpha_i y_i = 0, \quad C \geq \alpha_i \geq 0, \quad i = 1, 2, \ldots, N$$ $$\alpha^* = (\alpha_1^{\ast}, \alpha_2^{\ast}, \ldots, \alpha_N^{\ast})$$

• Calculate.

$$w^{\ast} = \sum_{i=1}^{N} \alpha_j^{\ast} y_i x_i$$ $$\forall C > \alpha_j^{\ast} > 0, \quad b^\ast = y_j - \sum_{i=1}^{N} \alpha_i^{\ast} y_i K(x_i \cdot x_j)$$

SMO Algorithm

Algorithm concept

SMO algorithm is a kind of heuristic algorithm.

Solution methods for quadratic programming with two variables

$$\begin{align} &\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i \\\\ &s.t. \quad \sum_{i = 1}^{N} \alpha_i y_i = 0, \quad C \geq \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \end{align}$$

We choose $\alpha_1, \alpha_2$, fixing other variables $\alpha_i (i = 3, 4, \dots, N)$.
Now, we solve following question:

$$\begin{align} &\min_{\alpha_1, \alpha_2} W(\alpha_1, \alpha_2) = \frac{1}{2} K_{11}\alpha_1^2 + \frac{1}{2} K_{22}\alpha_2^2 +y_1y_2K_{12}\alpha_1\alpha_2 - (\alpha_1 + \alpha_2) + y_1\alpha_1\sum_{i=3}^{N}y_i\alpha_iK_{i1} + y_2\alpha_2\sum_{i=3}^{N}y_i\alpha_iK_{i2} \tag{2} \\\\ &s.t. \quad \alpha_1y_1 + \alpha_2y_2 = \sum_{i=3}^{N}y_i\alpha_i = \zeta, \quad 0 \leq \alpha_i \leq C, \quad i = 1, 2 \tag{3} \end{align}$$

$K_{ij} = K(x_i, x_j),i,j = 1,2, \dots, N$, $\zeta$ is a constant, the constant term in $(2)$ is omitted.

We consider best optimal question about $\alpha_2$.

if $ y_1 \neq y_2 $.

$$L = max(0, \alpha_2^{old} - alpha_1^{old}), \quad H = min(C, C + \alpha_2^{old} - alpha_1^{old}) \tag{4}$$

else.

$$L = max(0, \alpha_2^{old} + alpha_1^{old} - C), \quad H = min(C, \alpha_2^{old} + alpha_1^{old}) \tag{5}$$ $$g(x) = \sum_{i=1}^{N}\alpha_i y_i K(x_i, x) + b$$ $$E_i = g(x_i) - y_i = \sum_{j=1}^{N}\alpha_j y_j K(x_j, x_i) + b - y_i, \quad i = 1, 2$$

Now, we update $\alpha_2$.

$$\alpha_2^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1 - E_2)}{\eta}, \quad \eta = K_{11} + K_{22} - 2K_{12}$$ $$\alpha_2^{new} = \begin{cases} H, &\alpha_2^{new,unc} > H \\ \alpha_2^{new,unc}, &L \leq \alpha_2^{new,unc} \leq H \\ L, &\alpha_2^{new,unc} < L \end{cases}$$

Next, update $\alpha_1$.

$$\alpha_1^{new} = \alpha_1^{old} + y_1 y_2(\alpha_2^{old} - \alpha_2^{new})$$

Solution methods for selecting variables

1. select the highest $E_i$ in all nodes as $\alpha_1$.
2. select the highest $|E_1 - E_2|$as $\alpha_2$.

Solution methods for calculating threshold b and E

$$b_1^{new} = -E_1 - y_1 K_{11} (\alpha_1^{new} - \alpha_1^{old}) - y_2 K_{21} (\alpha_2^{new} - \alpha_2^{old}) + b^{old}$$ $$b_2^{new} = -E_2 - y_1 K_{12} (\alpha_1^{new} - \alpha_1^{old}) - y_2 K_{22} (\alpha_2^{new} - \alpha_2^{old}) + b^{old}$$ $$b^{new} = \frac{b_1^{new} + b_2^{new}}{2}$$

What’s more

updating $E$.

$$E_i^{new} = \sum_{\mathcal{S}}y_j \alpha_j K(x_i, x_j) + b^{new} - y_i.$$

$\mathcal{S}$ includes all SV $x_i$.